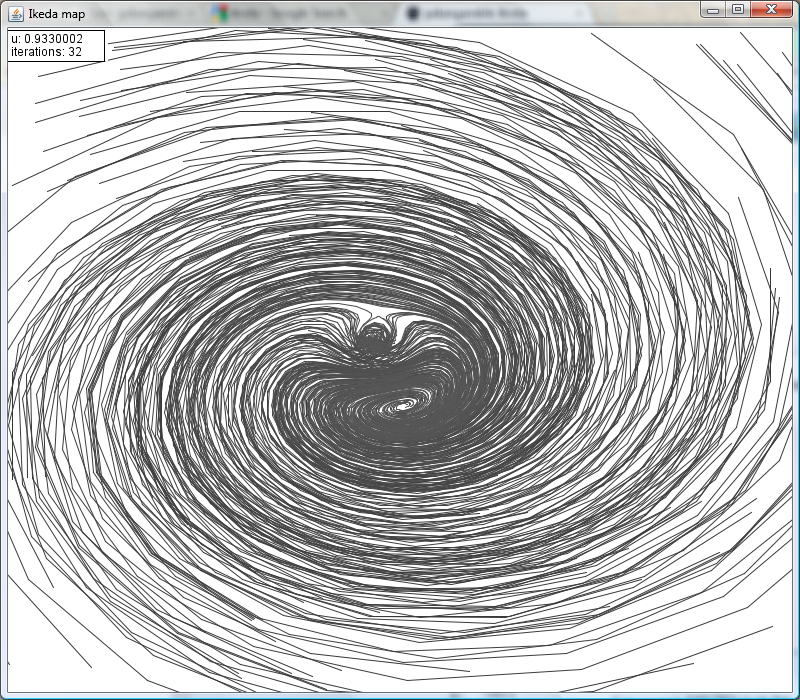
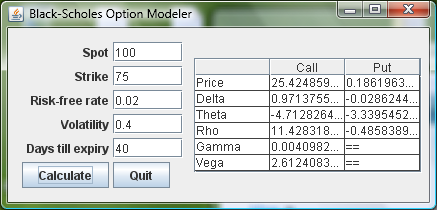
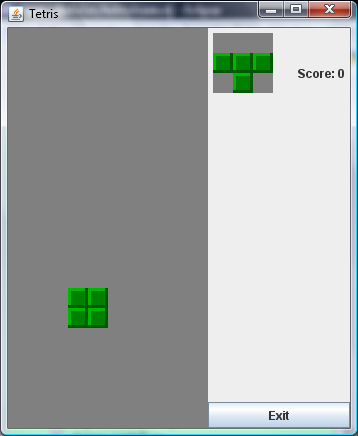
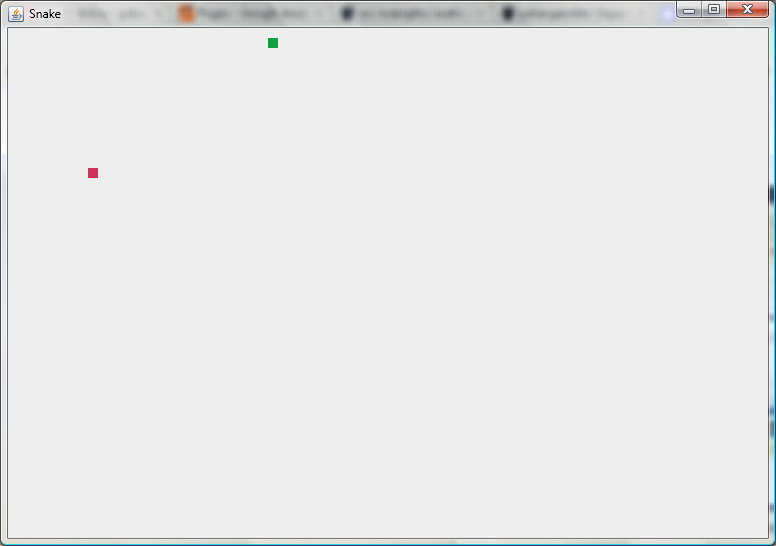
The Beauty of the mathematics of a sinkhole – captured in a Clojure GUI
Lau B. Jensen wrote an amazing blog post called Theory vs Clojure. Here he described how to develop in Clojure a discrete-time dynamic system called an Ikeda map.
Rich Hickey then submitted his improvements to the code. This demo is Rich Hickey’s version.
You can launch it via web start here. You can read the code here.